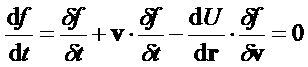13
On Model
Approaches
•Combes et al. approach the subject from the general case
of distribution functions (f) –
what are the positions, velocities,
and time of the stars moving in a potential?
•Can start with the continuity equation (mass) which is the collisionless Boltzmann equation, AKA the Vlasov equation:
•-dU/dr is the gravitational force exerted. The potential can be obtained from the Poisson eq: ΔU(r) =4πGρ(r). Must find f(r,v) that solves
these self-consistently. They discusses
the isothermal
sphere case:
–f(E)=(2πσ2)-3/2ρ0e -E/σ2 (complications
vanish in symmetry)
•Should be familiar-looking function. Still, want density as a function of radius.