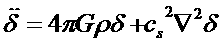Jeans Mass and the
Growth of Perturbations
Growth of Perturbations
Linearize the
equations and solve for ∆=∂ρ/ρ=∂ for an unperturbed solution
corresponding to a static, uniform fluid (constant pressure,
density, and zero velocity):
Where cs is the speed
of sound.
In the absence of a
pressure term, growth will be exponential with a time scale of tff ~ (Gρ)-1/2. The sound wave crossing time
is the so-called
Jeans length divided by the sound speed.
Equating the
two time scales gives LJ ~ cs (Gρ)-1/2 and the Jeans mass is just MJ ~ LJ3 ρ ~ cs3G-3/2ρ-1/2
The Jeans mass
is the minimum mass of a system for which the pressure cannot counteract the increase in
the density contrast.