


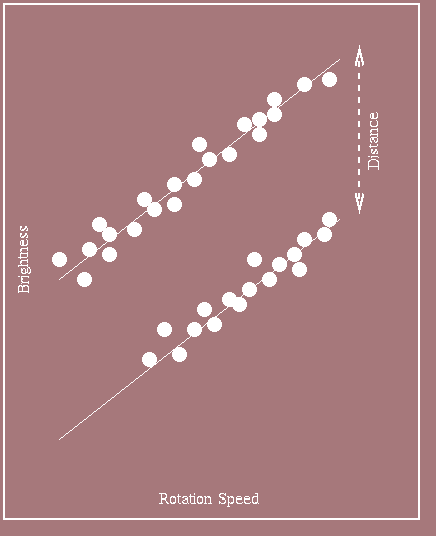
How Tully-Fisher works:
Spiral galaxies have a flattened shape due to the rapid rotation of the stars and gas as it orbits the galaxy. Typical speeds are about 200 km/sec allowing this motion to be easily measured via the Doppler shift. The light emitted by that portion of the galaxy moving away from us will be red-shifted while that portion approaching us will be blue shifted (top panel). The rotational speed of the stars and gas is nearly constant with radius within spiral galaxies (bottom panel). When a spectrum of is taken, the signal of a particular emission line (say from Hydrogen) will be spread in wavelength according to velocity. This Doppler broadening can then be measured to obtain the rotational speed of the galaxy. When the rotation speeds and the luminosities (intrinsic brightnesses) of spiral galaxies are plotted against each other (below)a strong trend is found. This is the relation known as the Tully-Fisher relation. Distances are measured from the difference in the apparent brightness of galaxies from those at known distance with the same rotaional velocity.

Some actual data:
Here is shown some actual data. The four panels show the Tully-Fisher relations which result for 4 different samples. The top left panel shows data for nearby galaxies whose distances are known. These are the local calibrators. Clockwise are shown the Ursa Major, Virgo, Pisces, and Coma clusters. Catalogs of galaxies are typlicaly limited to the apparent brightness so the more distant clusters become progressively more limited. Note the large scatter in the Virgo sample compared with the others. This is thought to originate from the line-of-sight depth within this complex region.

Expansion of the Universe:
When the Tully-Fisher relation is fit to each cluster the average distance can be computed. When these are plotted against the average velocity it is found that distance and velocity are proportional. This is the local velocity field and the slope of this relation is the Hubble Constant.![]() More Information
More Information
Links to related sites